This is a good question because it was unfamiliar to us before meeting students who were struggling with it. It looked like a trick or short form for something when first encountered. This is exactly what it is. Synthetic division is a shorthand for long division but in the special case of polynomial division when the divisor is a linear function of the form, x-a, where a is any real number. Not bx-a but specifically x-a.
Can synthetic division always be used a shorthand for long division?
No. For example, if the divisor is any other polynomial other than a linear function, synthetic division cannot be used. Regular long division must be used. If the divisor is a linear function NOT of the form x-a then synthetic division cannot be used.
So why use synthetic division?
Since it is a shorthand way of doing polynomial division in this one very specific case, it does save time and space when writing. As a result, it is a quick way to check for linear factors or roots of a polynomial.
How does synthetic division work?
This is a good question. Looking at a completed synthetic division problem, it does not look like much but a table of numbers. The best way to understand how synthetic division works is to go work through an example and then practice!
Let’s consider the following example.
Example
\frac{x^2 + 5x + 6}{x-1}
Our divisor is a linear function x-1 with leading coefficient equal to 1. This means we can use synthetic division.
Therefore, we have
\frac{x^2 + 5x+6}{x-1} = x+6 + \frac{12}{x-1} . We can also conclude that x-1 is not a root of x^2 + 5x + 6 .
Let’s try another example.
(x^4 – 3x^3 – 11x^2 + 5x + 17) \div (x+2)
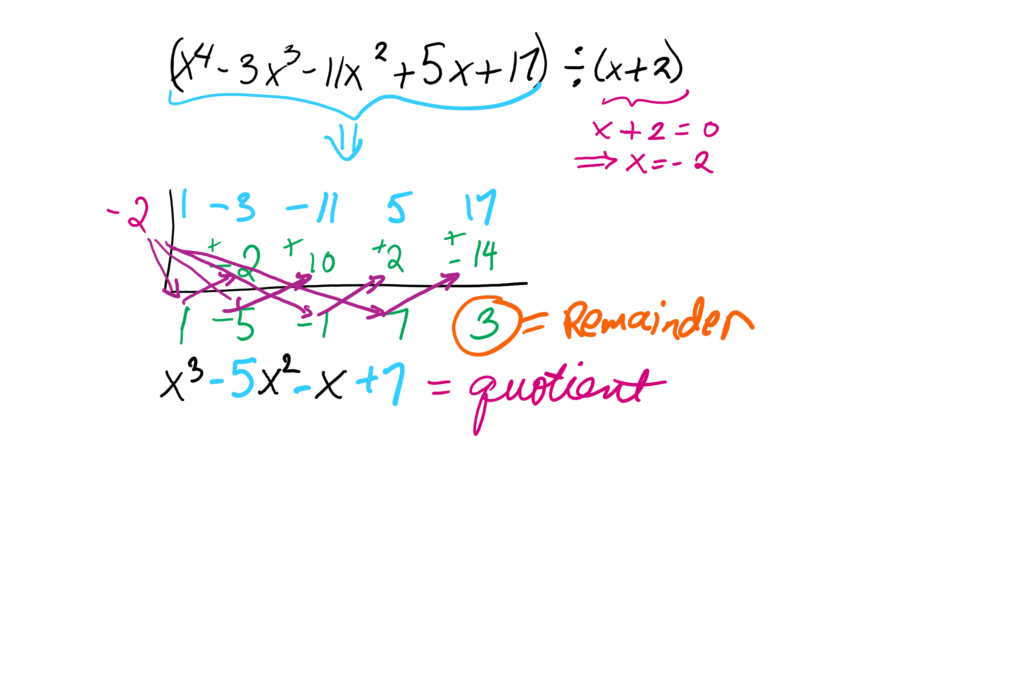
Therefore, we have
\frac{x^4 – 3x^3 – 11x^2 + 5x + 17}{x+2} = x^3 – 5x^2 – x + 7 + \frac{3}{x+2} .
From here we can conclude that x=-2 is not a zero of x^4 – 3x^3 – 11x^2 + 5x + 17
Let’s try another example, \frac{-x^5 + 1}{x+1}. We have a fifth degree polynomial as the dividend. We can also write -x^5 + 1 as, – x^5 + 0x^4 + 0x^3 + 0x^2 + 0x + 1
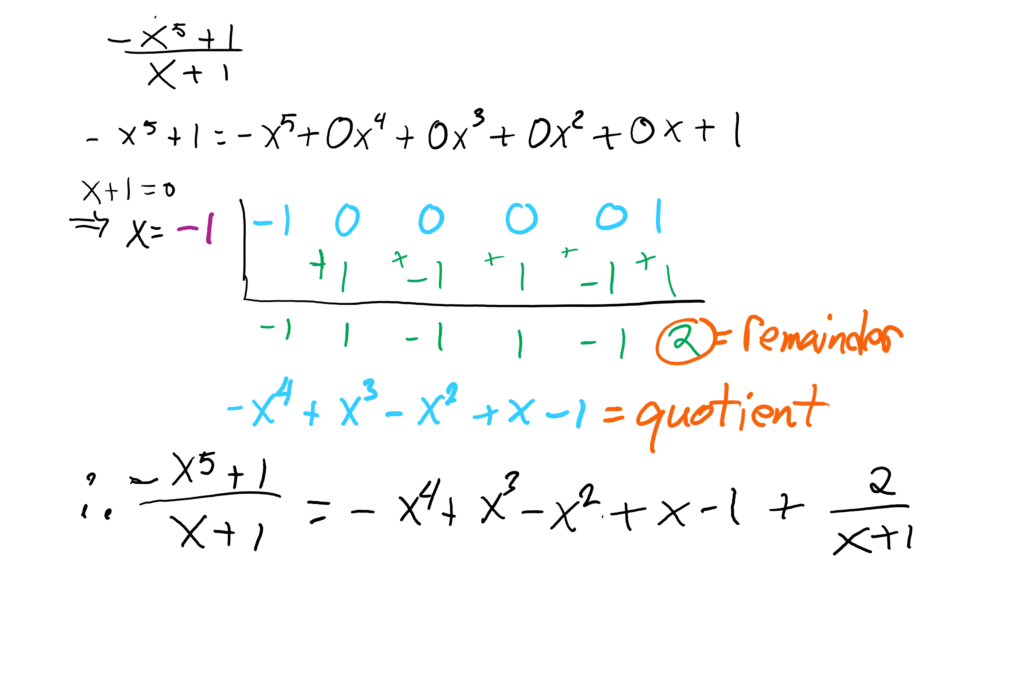
Therefore, \frac{-x^5 + 1}{x+1} = -x^4 + x^3 – x^2 + x – 1 + \frac{2}{x+1} and x=-1 is not a zero of -x^5 + 1.
Let’s try another example, \frac{-x^5 + 1}{x-1}.
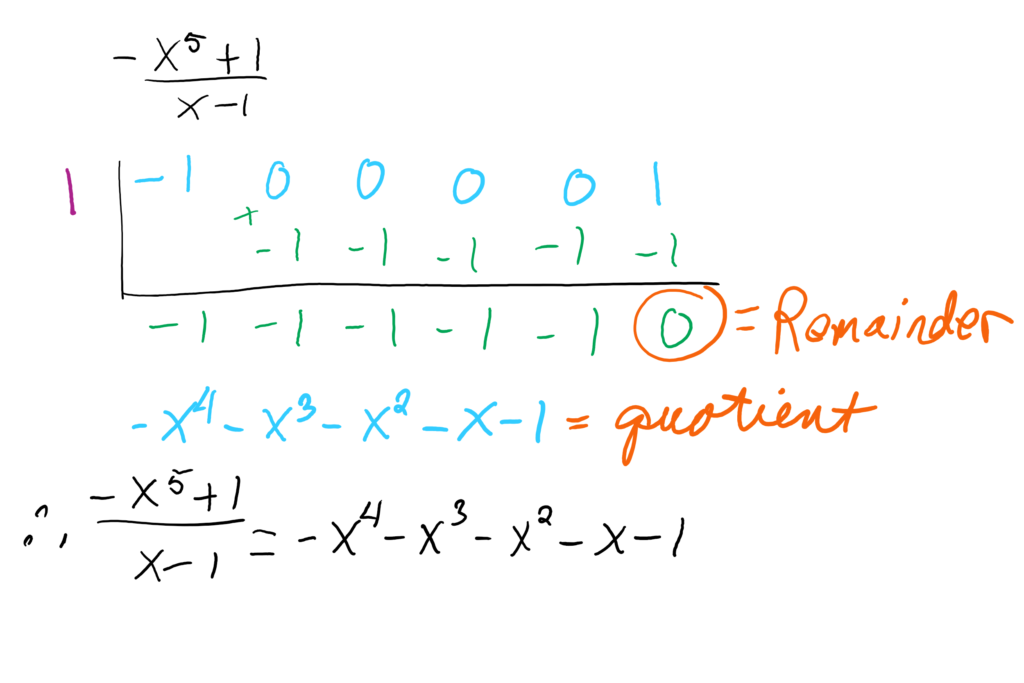
Therefore,
\frac{-x^5 + 1}{x-1} = -x^4 – x^3 – x^2 – x – 1
And since there is no remainder, x=1 is a zero of -x^5 + 1.
How does synthetic division compare to long division?
The best way to answer this question is to perform both types of division side by side and see what the difference is. Let’s consider the following example,
(2x^3 – 13x^2 + 17x – 10) \div (x-5) .
Let’s start with long division.
Therefore, (2x^3 – 13x^2 + 17x – 10) \div (x-5) = 2x^2 – 3x + 2 or 2x^3 – 13x^2 + 17x – 10 = (x-5)(2x^2 – 3x + 2) or x-5 is a linear factor of 2x^3 – 13x^2 + 17x – 10 and x=5 is a zero of 2x^3 – 13x^2 + 17x – 10.
Now let’s use synthetic division.
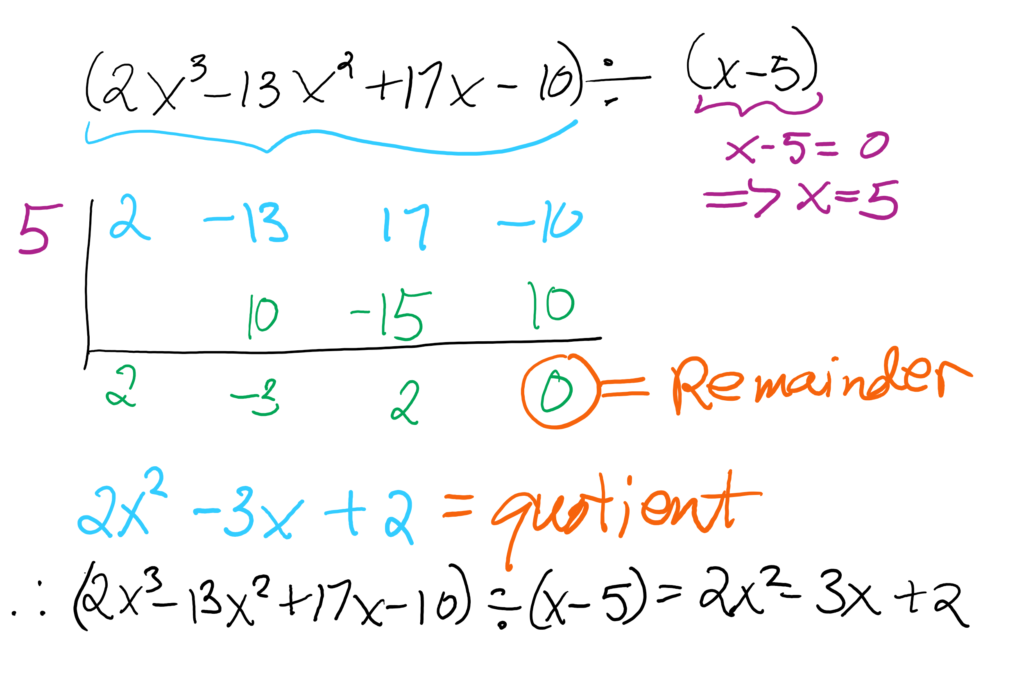
Therefore, x=5 is a zero of 2x^3 – 13x^2 + 17x -10 or
\frac{2x^3 – 13x^2 + 17x – 10}{x-5} = 2x^2 -3x + 2
Or 2x^3 – 13x^2 + 17x – 10 = (x-5)(2x^2 – 3x + 2) .
Long division does take up more space, but synthetic division is not as intuitive as to how to use it or interpret the result. It does require some practice. Let’s consider the following example.
Example: Perform the following polynomial division
(2x^5 – 5x^4 + 7x^3 + 4x^2 – 10x + 10) \div (x^3+2)
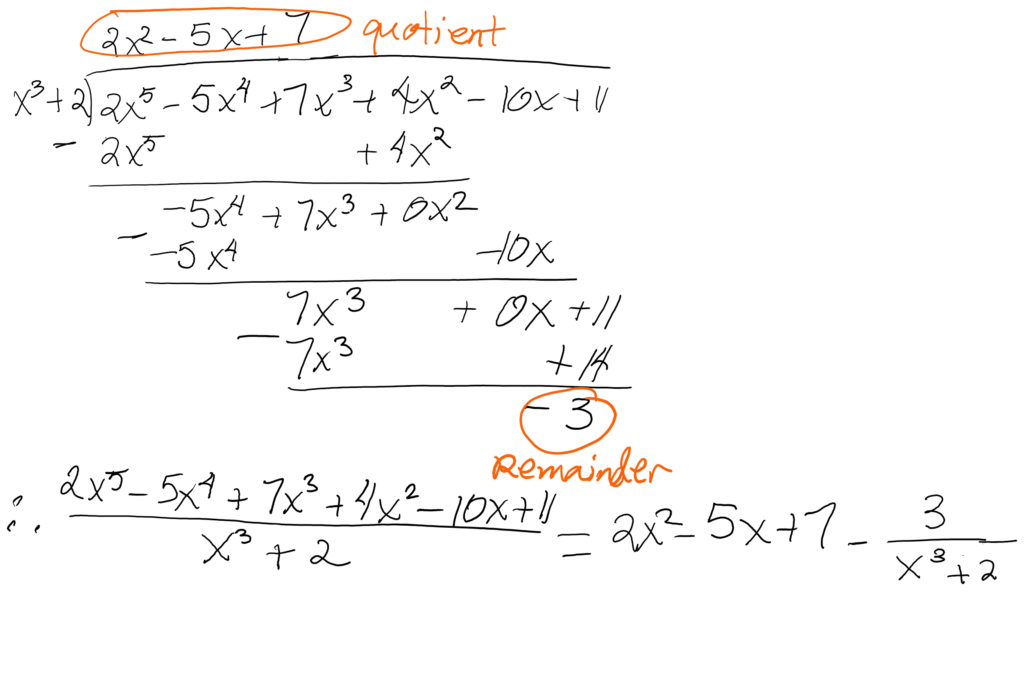
Solution:
Since the divisor is not linear, we need to use long division.
Therefore, (2x^5 – 5x^4 + 7x^3 + 4x^2 – 10x + 10) \div (x^3+2) = 2x^2 – 5x + 7 – \frac{3}{x^3 + 2}
Final thoughts:
It’s great for the special case of polynomial division when the divisor is a linear function of the form x-a. However, it is worthwhile learning and becoming comfortable with polynomial long division because as we see, there will be many more situation where the divisor is not a liner function and synthetic cannot be used.
Attached are some practice exercises for both types of division described above.
References
- Purplemath.com
- Tutorial.math.lamar.edu
- Storyofmathematics.com
- Mathbitsnotebook.com
