Discover how to find the area of a slice of pizza using math

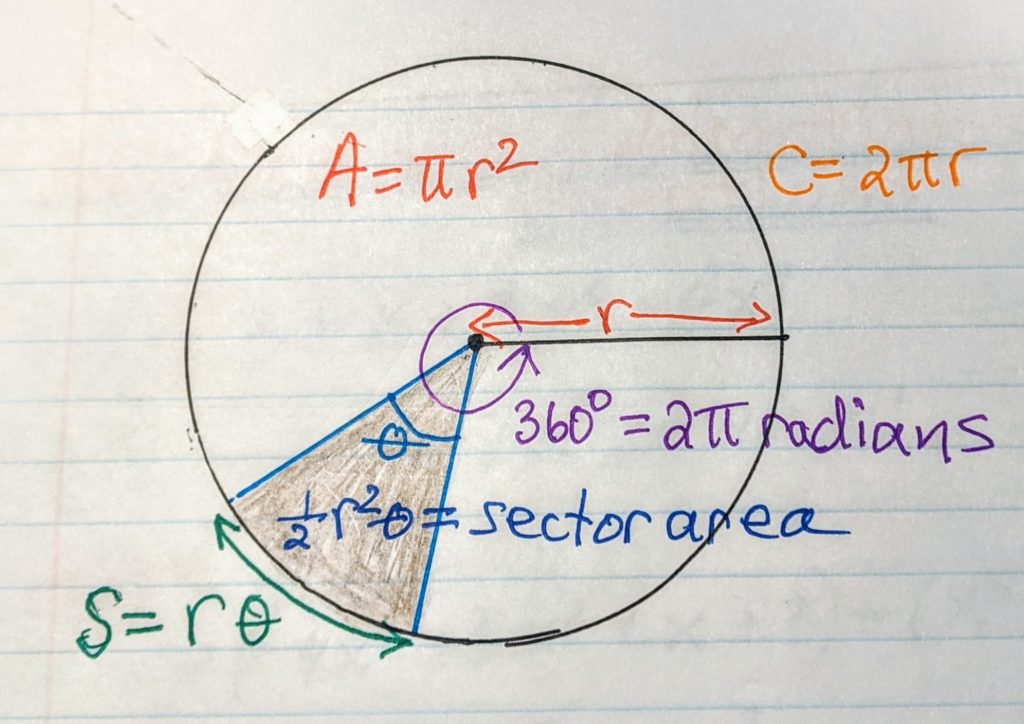
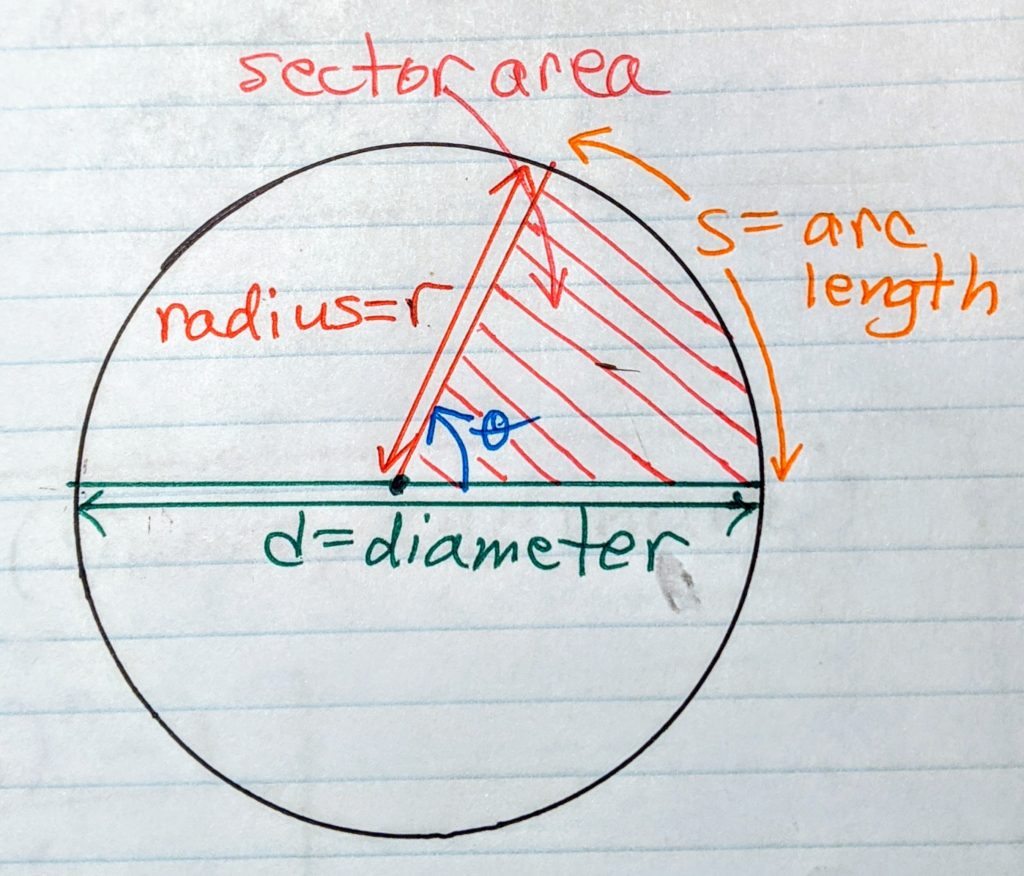
The arc length of a our slice of pizza or our sector is given by

\text{Arc Length} = s = r \theta 

And the sector area of our slice of pizza is given by,

\text{sector area} = = \frac{1}{2} r^2 \theta

This angle \theta  is given in the measure of radians. What is a radian?  \pi \text{ radians } = 180^\circ . Using this relation between radians and degrees we can convert any degree measure to radians and vice versa.  For example,

36^\circ = 36 \times \left ( \frac{\pi}{180} \right) \text{ radians}

Let’s consider an example.

Suppose we buy a medium pizza and we are really hungry and eat one third of the pizza.  How much pizza have we eaten?

Solution: 

So we know a medium pizza has a diameter of 12 inches.  This means the radius of the medium pizza is 6 inches, or r = 6”.  Next, we need to determine the central angle of our 1/3 slice or sector of the pizza.  We know that one revolution of a circle is 360^\circ .  We are only eating one third of the pizza so we are only going around one third of a full revolution about the centre of the pizza.  One third of 360^\circ is \frac{1}{3} \times 360^\circ = 120^\circ .  What is the radian measure of 120^\circ ?  120^\circ = 120 \times \left ( \frac{\pi}{180} \right) = \frac{2\pi}{3} \text{ radians} .  Now we have, r=6”, \theta = \frac{2\pi}{3} and we can calculate our sector area 

\text{ sector area }=\frac{1}{2}r^2 \theta = \frac{1}{2} (6^2) \left( \frac{2\pi}{3} \right) = 12 \pi \text{inches}^2   .   So the amount or area of the slice of pizza we ate was 12 \pi \text{ inches}^2

Let’s take a look at a few exercises related to our pizza and see how much pizza we can eat.